자료구조/👉알고리즘 - 21

오늘 들은 강의 목록

1. 그래프 최단 경로 - 2
2. 다익스트라 - 1

다익스트라 알고리즘

다익스트라 알고리즘을 여러가지 방법으로 구현할 수 있는데,
그 중 가장 개선된 우선순위 큐를 사용하여 구현할 것이다.

1. 초기화 : 시작점에서 모든 노드까지 가는데 드는 비용을 무한대로 초기화
2. 시작 : 시작노드까지 가는데 드는 비용을 0으로 설정, 우선순위 큐에 넣는다.
3. 우선순위 큐에서 가장 위에 있는 값을 꺼내 현재 노드로 지정
4. 현재 노드에서 다음 노드(인접노드중 하나)로 가는 비용이
   기존에 다음 노드까지 가는데 드는 비용보다 적으면 비용을 업데이트하고, 우선순위 큐에 넣는다.
5. 3 ~ 4를 반복한다.

이때 우선순위 큐 구현은 최소 힙을 사용한다.

다익스트라 구현

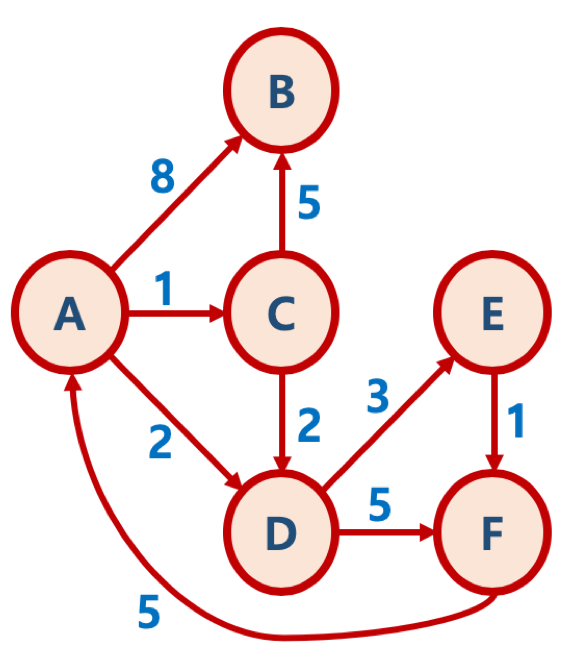
graph = {
    'A': {'B': 8, 'C': 1, 'D': 2},
    'B': {},
    'C': {'B': 5, 'D': 2},
    'D': {'E': 3, 'F': 5},
    'E': {'F': 1},
    'F': {'A': 5}
}
def dijkstra(graph, start):
    distance = {node : math.inf for node in graph}
    q = []
    distance[start] = 0
    heapq.heappush(q, [0, start])
    while q:
        curDist, curNode = heapq.heappop(q)
        nextNodes = graph[curNode]
        for nextNode in nextNodes:
            if distance[nextNode] > curDist + graph[curNode][nextNode]:
                distance[nextNode] = curDist + graph[curNode][nextNode]
                heapq.heappush(q, [distance[nextNode], nextNode])
    return distance
dijkstra(graph, 'A')

노드 A를 시작으로 모든 노드에 대해서 탐색하고,
모든 노드에 대해 길이를 반환하도록 했다.

여기까지가 기본적인 우선순위 큐를 이용한 코드다.

다익스트라 최적화

위 구현에서 우선순위 큐에 비용은 다르고 중복되는 노드가 들어갔을 때,
인접노드에 대한 계산이 두번된다.
비용이 적은 노드를 1, 비용이 더 큰 노드를 2라고 할 때,
1번이 먼저 계산되어 이후 비용이 1과 같게 된다.
이를 이용해 우선순위 큐에서 해당 노드까지 가는데 드는 비용을 기존에 드는 비용과 비교하여,
기존에 드는 비용이 더 싼 경우, 인접노드를 탐색하지 않고 건너뛰도록 한다.

우선순위 큐에서 꺼낸 노드의 현재 비용과, 기존 비용을 비교하여
현재 비용이 더 비싼 경우 건너뛴다.

def dijkstra(graph, start):
    distance = {node : math.inf for node in graph}
    q = []
    distance[start] = 0
    heapq.heappush(q, [0, start])
    while q:
        curDist, curNode = heapq.heappop(q)
        if distance[curNode] < curDist: # 최적화
            continue
        nextNodes = graph[curNode]
        for nextNode in nextNodes:
            if distance[nextNode] > curDist + graph[curNode][nextNode]:
                distance[nextNode] = curDist + graph[curNode][nextNode]
                heapq.heappush(q, [distance[nextNode], nextNode])
    return distance

다익스트라 최단 경로

def dijkstra(graph, start, end):
    distance = {node : math.inf for node in graph}
    prevNode = {node: None for node in graph}
    q = []
    distance[start] = 0
    prevNode[start] = start
    heapq.heappush(q, [0, start])
    while q:
        curDist, curNode = heapq.heappop(q)
        if distance[curNode] < curDist: # 최적화
            continue
        nextNodes = graph[curNode]
        for nextNode in nextNodes:
            if distance[nextNode] > curDist + graph[curNode][nextNode]:
                distance[nextNode] = curDist + graph[curNode][nextNode]
                prevNode[nextNode] = curNode # "현재노드에서 다음노드로 갔다"를 저장
                heapq.heappush(q, [distance[nextNode], nextNode])
    route = ''
    curNode = end
    while curNode != start:
        route += curNode + " <- "
        curNode = prevNode[curNode]
    route += curNode
    return [route, distance]
dijkstra(graph, 'A', 'F')