자료구조/👉알고리즘 - 22

오늘 들은 강의 목록

1. 그래프 탐색 - 시간복잡도
2. 최소 신장 트리 - 1

다익스트라 시간복잡도

1. 모든 노드에서 인접 노드에 가는데 걸리는 시간을 체크 : $O(E)$
   각 간선에 대해 한번씩 탐색하기 때문
2. 우선순위 큐에 push/pop : $O(E log E)$
   노드를 삽입하기 위해서는 각 간선들을 방문하는데, 각 간선들을 한번씩만 방문하기때문에 최대 $O(E)$,
   $O(E)$개의 노드가 삽입되어 있을때, 우선순위 큐의 시간복잡도 $O(log E)$로
   “노드의 수 * 우선순위 큐 시간복잡도”가 된다. -> $O(E * log E)$
   따라서 다익스트라 알고리즘의 시간복잡도는 $O(E) + O(E log E) = O(E log E)$ 이다.

다익스트라 노드/간선 방문횟수 확인

def dijkstra(graph, start, end):
    distance = {node : math.inf for node in graph}
    prevNode = {node: None for node in graph}
    q = []
    distance[start] = 0
    prevNode[start] = start
    heapq.heappush(q, [0, start])
    visitedEdgeCnt = 0 # 방문한 간선 수 초기화
    while q:
        curDist, curNode = heapq.heappop(q)
        if distance[curNode] < curDist: # 최적화
            continue
        print("visit : ", curNode) # 현재 방문한 노드 (최적화로 인접노드를 방문하지 않는 경우는 계산하지 않는다)
        visitedEdgeCnt += len(graph[curNode]) # 방문한 간선 수 계산
        nextNodes = graph[curNode]
        for nextNode in nextNodes:
            if distance[nextNode] > curDist + graph[curNode][nextNode]:
                distance[nextNode] = curDist + graph[curNode][nextNode]
                prevNode[nextNode] = curNode # "현재노드에서 다음노드로 갔다"를 저장
                heapq.heappush(q, [distance[nextNode], nextNode])
    route = ''
    curNode = end
    while curNode != start:
        route += curNode + " <- "
        curNode = prevNode[curNode]
    route += curNode
    return [route, distance, visitedEdgeCnt]
                
dijkstra(graph, 'A', 'F')

노드 방문은 A에서 F까지 모든 노드를 한번씩 방문했다.
같은 노드에 대해 이미 더 짧은 경로를 찾아 인접노드를 방문하지 않는 경우,
연산을 하지 않기 때문에 출력되지 않는다.

간선 방문 횟수는 9로, 모든 간선의 수와 같다.(사진에서 빨간 줄 친 부분)

신장 트리(Spanning Tree)

스패닝 트리(신장트리)는 어떤 그래프가 주어질 때,
해당 그래프의 모든 노드가 연결되면서, 트리의 속성을 만족하는 그래프다.

신장트리가 되기 위한 조건

• 원래 그래프의 모든 노드를 포함
• 모든 노드가 연결됨
• 사이클이 생기지 않아야함

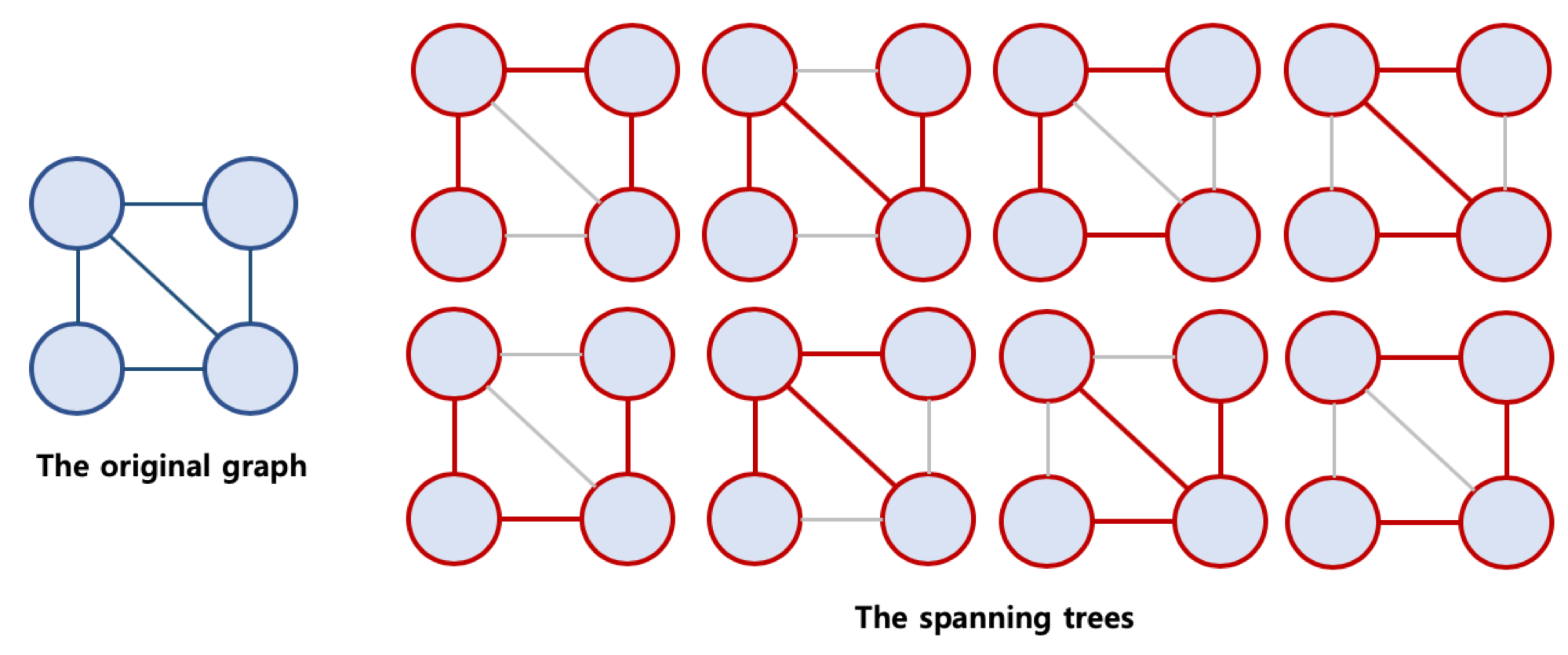
한 그래프에서 나타낼 수 있는 여러가지 스패닝 트리들

최소 신장 트리 (Minimum Spanning Tree, MST)

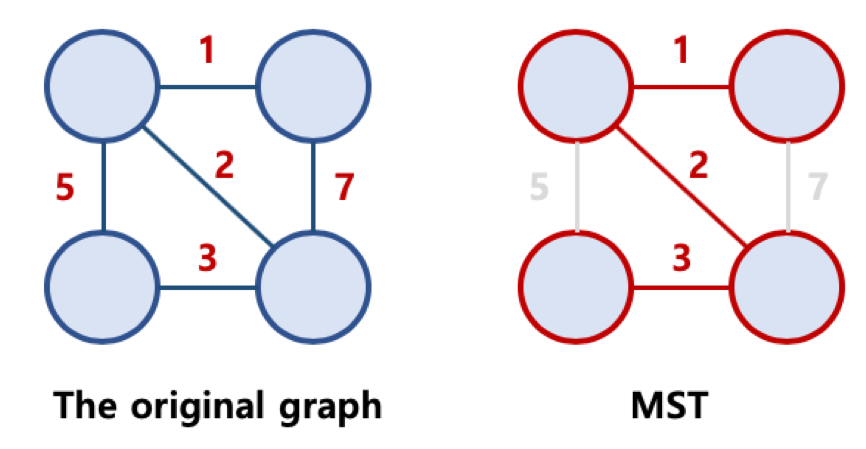
MST는 간선의 가중치 합이 최소인 스패닝 트리를 말한다.

최소 신장 트리 알고리즘

• 크루스칼 알고리즘(Kruskal)
• 프림 알고리즘(Prim)

마지막

7일에 포스트 작성하고, 패캠에 안 올렸다가 챌린지 끊길뻔했다.
깜박하지 말아야지 :)