자료구조/👉알고리즘 - 20

오늘 들은 강의 목록

1. 그리디 - 2
2. 그래프 최단경로 - 1

그리디(부분 배낭 문제, fractional knapsack problem)

무게제한이 $k$인 배낭에 최대 가치를 가지도록 물건을 넣는 문제
물건은 무게 $w$와 가치 $v$를 가짐
물건을 쪼개서 넣기 가능하다. (쪼개서 못넣는 경우의 문제를 0/1)

stuffs = [
    {"weight": 10, "value": 10},
    {"weight": 15, "value": 12},
    {"weight": 20, "value": 10},
    {"weight": 25, "value": 8},
    {"weight": 30, "value": 5},
]
def FractionalKnapsack(maxweight, stuffs):
    stuffs = sorted(stuffs, key=lambda x:x["weight"]/x["value"])
    value = 0
    for stuff in stuffs:
        if maxweight - stuff['weight'] < 0:
            value += stuff['value'] / stuff['weight'] * maxweight
            break
        else:
            value += stuff['value']
            maxweight -= stuff['weight']
    return value
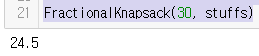
FractionalKnapsack(30, stuffs)

제한된 무게로 최고의 가치를 얻는 방법은
“무게 1당 가치”가 가장 큰 것들을 고르면 된다.

따라서 무게/가치에 따라서 물건들을 정렬하고
앞에서부터 하나씩 가방에 채워나간다.
다음으로 넣을 물건이 넣을 수 있는 무게보다 적으면, 물건을 쪼개서 넣는다.

그리디의 잘못된 사용(?)

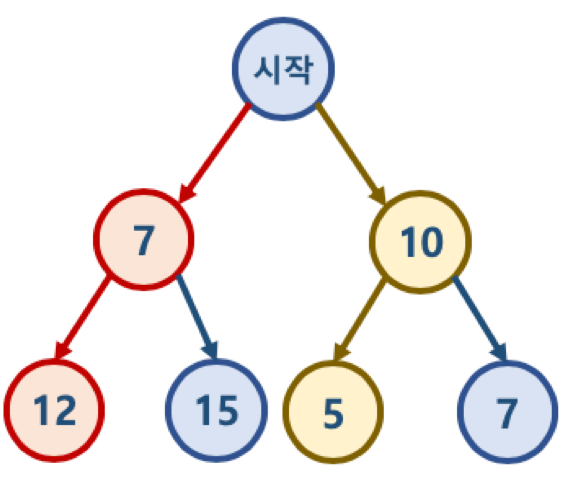
트리에서 최소가 되도록 고르는 방법을 구하는 문제
위 그림에서 매 순간 선택지 중 가장 최적의 답을 골랐을 때,
$7 + 12 = 19$가 되는데
올바른 답은 $10 + 5 = 15$가 최소가 된다.

단순하게 완전탐색을 통해서 선택할 수 있는 모든 방법으로 선택했을 때,
결과값들을 비교해서 최소의 값을 구할 수 있다.

최단 경로 알고리즘

두 노드를 잇는 가장 짧은 경로를 찾는 방법

가중치 그래프에서 간선의 가중치 합이 최소가 되도록 하는 경로를 찾는 방법

문제 종류

1. 단일 출발 단일 도착
   특정 노드에서 출발해서 특정 노드에 도착하는 문제. (u -> v)
2. 단일 출발
   특정 노드에서 다른 모든 노드에 대해서 가장 짧은 경로를 찾는 문제 (u -> 모든 노드)
3. 전체 쌍 모든 쌍에 대한 최단경로를 찾는 문제 (모든 노드 -> 모든 노드)

다익스트라 알고리즘 (Dijkstra)

연결되어있는 노드들을 탐색하며, 시작 노드에서 각 노드까지의 최단거리를 갱신

처음에 시작 노드까지 가는 비용을 0, 다른 모든 노드들로 가는 비용을 무한대로 초기화
시작 노드를 현재노드로 해서 시작.
현재노드의 인접노드들을 탐색해서, 현재 노드에서 인접노드에 도달하는 비용이 기존에 다른 노드에서 인접노드에 도달하는데 드는 비용보다 적다면, 비용을 업데이트 한다. 이를 계속 반복하면 다익스트라 알고리즘이다.

마지막

다익스트라 알고리즘은 기억하는대로 써봤는데, 다음 강의 들을 때 확인해봐야겠다.
-끝-