자료구조/👉알고리즘 - 28

오늘 들은 강의 목록

1. 개선 프림 - 2
2. 백트래킹

개선된 프림알고리즘 시간복잡도

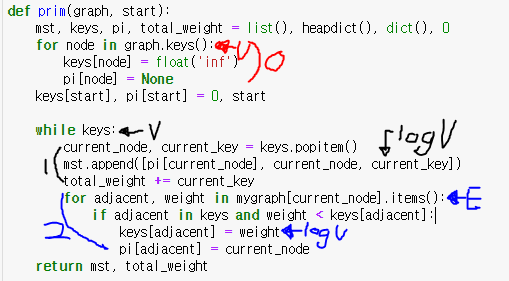
강죄에서 사용하는 코드를 기준으로 시간복잡도를 계산해보겠다

from heapdict import heapdict

def prim(graph, start):
    mst, keys, pi, total_weight = list(), heapdict(), dict(), 0
    for node in graph.keys():
        keys[node] = float('inf')
        pi[node] = None
    keys[start], pi[start] = 0, start

    while keys:
        current_node, current_key = keys.popitem()
        mst.append([pi[current_node], current_node, current_key])
        total_weight += current_key
        for adjacent, weight in mygraph[current_node].items():
            if adjacent in keys and weight < keys[adjacent]:
                keys[adjacent] = weight
                pi[adjacent] = current_node
    return mst, total_weight

mygraph = {
    'A': {'B': 7, 'D': 5},
    'B': {'A': 7, 'D': 9, 'C': 8, 'E': 7},
    'C': {'B': 8, 'E': 5},
    'D': {'A': 5, 'B': 9, 'E': 7, 'F': 6},
    'E': {'B': 7, 'C': 5, 'D': 7, 'F': 8, 'G': 9},
    'F': {'D': 6, 'E': 8, 'G': 11},
    'G': {'E': 9, 'F': 11}    
}
mst, total_weight = prim(mygraph, 'A')
print ('MST:', mst)
print ('Total Weight:', total_weight)

1. 초기화 구간 -> $O(V)$
2. 힙에서 pop하는 구간 -> $O(V log V)$
   힙에서 pop : $O(log V)$ (keys.popitem)
   위 연산을 하는 횟수 : $V$ (while keys)
3. 인접노드를 통해 힙을 업데이트 하는 구간 -> $O(E log V)$
   힙을 업데이트 : $O(log V)$ (keys[adjacent] = weight)
   위 연산을 하는 횟수 : $O(E)$ (for … in mygraph[current_node].items())

따라서 시간복잡도는 $O(V + V log V + E log V)$로
$O(E log V)$가 된다.

$O(E log V) < O(E log E)$는 $V \le E$가 보장되기 때문

백트래킹 기법

제약 조건 만족 문제에서 해를 찾기 위한 기법

해를 찾기 위해 조건을 체크하면서 넘어가고, 조건에 해당하지 않는 경우, 다음에 다시 방문하지 않도록 체크해두는 기법

구현시, 모든 경우의 수를 상태공간 트리를 통해 표현하고,
dfs하면서 조건이 맞는지 검색하고(Promising),
조건에 해당하지 않는다면 더 깊이 탐색하지 않고, 다른 탐색지점으로 간다.(가지치기, Pruning)

상태공간트리 : 문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리
(이건 아직 잘 모르겠다??)

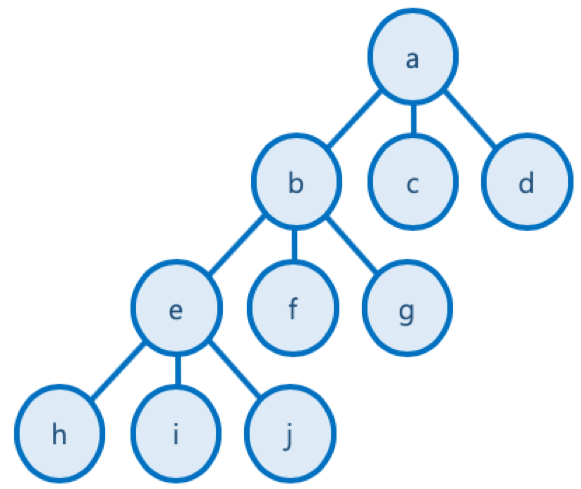
마지막

백트래킹도 쓸일많아서 잘 알아둬야한다.