자료구조/👉알고리즘 - 27

오늘 들은 강의 목록

1. 프림 - 4
2. 개선 프림 - 1

프림 시간복잡도

while connected_e:
    next_e = heappop(connected_e)
    if next_e[2] not in connected_n:
        tree.append(next_e)
        connected_n.add(next_e[2])
        for edge in edgesOf[next_e[2]]: # E, 다 추가
            if edge[2] not in connected_n:
                heappush(connected_e, edge) # log E

모든 간선 추가 -> $E$

힙 push -> $log E$

시간복잡도 : $O(E log E)$

프림 알고리즘 개선

대부분 $O(E log V)$의 시간복잡도를 가지는 프림 알고리즘

간선이 아닌 노드를 중심으로 우선순위 큐를 적용

1. 힙에 모든 노드를 넣고, key는 무한대로 초기화 (key = 가중치)
2. 힙에 있는 시작 노드의 key를 0으로 초기화(heapdict를 이용, decrease-key)
   이때 이전 노드를 저장할때 이전노드를 시작노드로 한다.
3. 힙에서 노드를 뽑고, 선택한다.
4. 선택한 노드에 연결된 간선들에 대해 5번을 진행한다.
5. 각 간선에 연결된 노드를 확인하고,
   해당 간선의 가중치가 힙에 있는 해당 노드의 가중치보다 작으면, 힙의 가중치를 업데이트 한다.
6. 힙에 노드가 없을 때까지 3번~5번을 반복한다.

from heapdict import heapdict
def advprim(edges, start_node):
    tree = []
    # 각 노드별로 연결된 간선을 정리
    # 그래프 구조를 만들때 이런 구조로 만드는게 국룰이지만 이전코드 재사용하느라..
    edgesOf = defaultdict(list)
    for weight, n1, n2 in edges:
        edgesOf[n1].append((weight, n1, n2))
        edgesOf[n2].append((weight, n2, n1))
    # 노드가 들어있는 힙 초기화
    n_heap = heapdict()
    for node in edgesOf:
        n_heap[node] = float('inf')
    n_heap[start_node] = 0
    before = {node : None for node in edgesOf}
    before[start_node] = start_node
    
    while n_heap:
        cur_n, cur_k = n_heap.popitem()
        prev_n = before[cur_n]
        tree.append([prev_n, cur_n, cur_k])
        for w, c, n in edgesOf[cur_n]:
            if n in n_heap and w < n_heap[n]:
                n_heap[n] = w
                before[n] = cur_n
        
    return tree

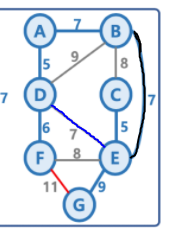
실행 결과는 이전에 기본 프림 알고리즘과는 조금 다르게 나왔다.

검은색으로 칠한 7의 가중치를 가진 간선 대신,
파란색으로 칠한 7의 가중치를 가진 간선이 추가되었다.
그러나 가중치가 같아서 mst의 가중치 합은 같다.

heapdict?

힙 구조에서 이미 삽입되어있는 노드의 key가 변경되었을 때, 힙 구조가 변경되어야 할 때를 위해 사용하는 모듈
우선순위가 변경되어도 힙 구조를 유지한다.(decrease-key)

hd = heapdict()
hd[obj1] = priority1
hd[obj2] = priority2
print(hd.peakitem())
(obj, priority) = hd.popitem()

위의 예시처럼 사용할 수 있다.

마지막

프림 알고리즘은 처음구현해봐서 강의에서 주어진 코드를 참고했다.
그리고 주석으로 작성했듯이 그래프 구조를 구현할 때,(함수에 넘겨주기 전에)
구조를 잘 만들어서 함수 내에서 다시 고치지 않도록 하는게 좋다고 생각한다.