자료구조/👉알고리즘 - 13

학습기록

오늘 들은 강의 목록

1. 동적계획법과 분할
2. 퀵 정렬

동적계획법(DP, Dynamic Programming)

하나의 큰 문제를 부분문제로 나누어서 부분문제를 해결하고,
부분문제의 해를 이용해서 큰 문제를 해결하는 방식.
상향식 접근법(Top-Down)

fibo(5)를 구할때,
fibo[0] -> fibo[1] -> fibo[2] -> fibo[3] -> fibo[4] -> fibo[5] 이런 순서로 구한다.
따라서, 아래애서 위를 향한 형태를 띄어서 상향식 접근법이라고 한다.
대부분 반복문으로 구현된다.

메모이제이션(Memoization)

이전에 계산한 값을 저장하여, 같은 문제에 대해 다시 계산하지 않도록 하는 방법

분할 정복(Divide and Conquer)

문제를 나눌 수 없을 때까지 나누어서 해결하고, 그것들을 다시 합병하여서 해결하는 방법
하향식 접근법(Bottom-Up)

fibo(5)를 구할때 fibo(5) -> fibo(4) -> fibo(3) -> fibo(2) -> fibo(1) -> fibo(0) 이런 순서로 구하고 하위 문제의 결과값을 합쳐서 문제를 해결한다.
대부분 재귀함수로 구현된다.

피보나치 (기본)

callcnt = 0
def fibo(n):
    global callcnt
    callcnt += 1
    if n <= 1:
        return n
    return fibo(n - 1) + fibo(n - 2)

print(fibo(10), " , 호출횟수 : ", callcnt)

이 코드에서 연산횟수는 177번이다.

피보나치 수열을 구하는 함수를 DP, 분할정복으로 풀어보면 아래와 같다.

피보나치 (DP)

callcnt = 0
n = 10
memo = [None for i in range(n + 1)]
memo[0] = 0
memo[1] = 1
for i in range(2, n + 1):
    callcnt += 1
    memo[i] = memo[i - 1] + memo[i - 2]
print(memo[n], " , 호출횟수 : ", callcnt)

이 코드에서는 9회의 연산으로 해결되었다.

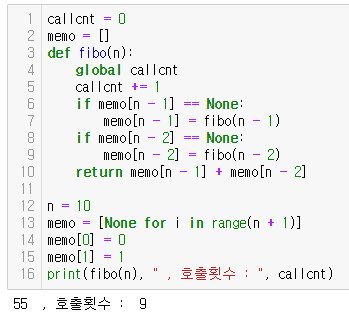
피보나치 (분할정복)

callcnt = 0
memo = []
def fibo(n):
    global callcnt
    print(n)
    callcnt += 1
    if memo[n - 1] == None:
        memo[n - 1] = fibo(n - 1)
    if memo[n - 2] == None:
        memo[n - 2] = fibo(n - 2)
    return memo[n - 1] + memo[n - 2]

n = 10
memo = [None for i in range(n + 1)]
memo[0] = 0
memo[1] = 1
print(fibo(n), " , 호출횟수 : ", callcnt)

이 코드에서도 9회의 연산으로 해결되었다.

피보나치 (단순재귀, DP, 분할정복) 비교

——-	단순재귀	DP	분할정복
연산횟수	177	9	9

메모이제이션 기법을 사용해서 연산횟수가 획기적으로 줄었다.

퀵 정렬(quick sort)

피봇(pivot, 기준점)을 정해서 기준점보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 정렬하는 것을 반복해서 정렬함.

1. 피봇을 정해서 피봇보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 정렬한다.
2. 왼쪽으로 나뉜 부분에서 피봇을 정해서 1을 수행한다.
3. 오른쪽으로 나뉜 부분에서 피봇을 정해서 1을 수행한다.

구현

def qsort(list):
    if len(list) <= 1:
        return list
    pivot = list[0]
    ll, rl = [], []
    for i in range(1, len(list)):
        if list[i] < pivot:
            ll.append(list[i])
        else:
            rl.append(list[i])
    return qsort(ll) + [pivot] + qsort(rl)

print(checkSortFunc(qsort))

퀵소트를 구현해봤는데 간단하게 된다?
아 파이썬 달다 달아~

시간복잡도

깊이 $log n$ : 각 단계로 내려갈때 둘로 나뉘기 때문에($log_2 n$),
각 단계당 약$n$번의 비교,
따라서 평균적인 시간복잡도는 $O(n log n)$이다.
(대부분 이걸 퀵소트의 시간복잡도라고 하고, 최악의 경우도 꼭 알아둬야한다.)
다만 최악의 경우에는 $O(n^2)$.

최악의 경우는 이미 정렬되어있는 경우다.

마지막

(TMI : c++ 알고리즘 헤더파일의 sort함수는 quicksort, heapsort, insertionsort(삽입정렬) 세가지로 구현된 Introsort로 구현되어있다.)