👉자료구조/👉알고리즘 - 12

학습기록

오늘 들은 강의 목록

1. 재귀 - 2
2. 재귀 - 3

재귀 함수

재귀 함수는 자기 자신을 호출하는 함수를 말한다.

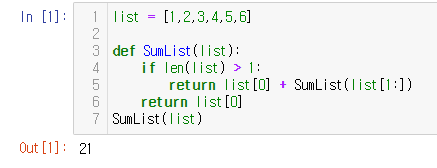
재귀함수 (리스트의 합)

list의 0번째 요소 + 슬라이싱을 이용해서 list의 1번째 요소부터 마지막 요소까지 이루어진 리스트 list[1:]를 SumList에 넘긴 결과값을 이용해서 작성했다.

list = [1,2,3,4,5,6]

def SumList(list):
    if len(list) > 1:
        return list[0] + SumList(list[1:])
    return list[0]
SumList(list)

시간복잡도 : $O(n)$
공간복잡도 : $O(n^2)$

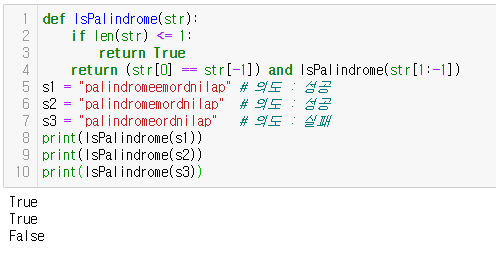
재귀함수 (회문 판별)

def IsPalindrome(str):
    if len(str) <= 1:
        return True
    return (str[0] == str[-1]) and IsPalindrome(str[1:-1])

시간복잡도 : $O(n)$
공간복잡도 : $O(n^2)$

재귀함수 (n을 1, 2, 3으로 나타낼 수 있는 경우의 수)

called = 0
def comb(n):
    print("comb : ", n)
    global called
    called += 1
    if n == 1:
        return 1
    elif n == 2:
        return 2
    elif n == 3:
        return 4
    return comb(n - 1) + comb(n - 2) + comb(n - 3)

n = 10
print(comb(n), " : ",called)

시간복잡도 : 약 $O(2^n)$ (계산을 어떻게 해야할지.. 그냥 n에 따라서 호출횟수를 다른 그래프랑 비교해봄) 공간복잡도 : 시간복잡도정도? 엄청 크다

함수 호출 횟수는 n이 10일때, 157번이다.

최적화(메모이제이션, 나중에 DP부분에서 나옴)

여러번 구하는 값을 메모해두고 다음에 필요할때 계산하지 않고 꺼내서 쓴다.

comb(8) -> comb(7), comb(6), comb(5)
comb(7) -> comb(6), comb(5), comb(4)
comb(6) -> comb(5), comb(4), comb(3)
comb(5) -> comb(4), comb(3), comb(2)
comb(4) -> comb(3), comb(2), comb(1)
comb(3) -> comb(2), comb(1)
comb(2) -> comb(1)

위에서 보면 comb(8)에서 comb(7), comb(6), comb(5)를 호출하는데,
comb(7)에서 comb(6), comb(5)를 다시 호출하게 된다.
이렇게 중복되는 계산이 많아서 사용하는 것이 메모이제이션인데,
메모이제이션을 통해서 중복되는 계산을 획기적으로 줄일 수 있다.

메모이제이션을 통해서 중복되는 계산을 줄이면
각 함수를 한번씩만 호출하면 그 후에는 계산할 필요 없이 memo에 저장된 값을 이용하면 된다.

시간복잡도 : $O(n)$
공간복잡도 : $O(n)$
함수 호출 횟수는 n이 10일때, 7번이다.

마지막

DP가 한 강좌로 구성되어있는데, 이게 맞나 싶다.
뒤에 다른 강의에서 같이 병행할 것 같기도 하고,
아니면 알고리즘 면접 등에서는 잘 안나오나? 싶기도?
(알고리즘 대회에는 단골이던데..)