자료구조/👉알고리즘 - 25

오늘 들은 강의 목록

1. 크루스칼 - 2
2. 프림 - 1

union-by-rank와 path-compression이 구현된 Union/Find(준비)

from string import ascii_uppercase
parentOf = {v : v for v in ascii_uppercase[:6]}
rank = {v : 0 for v in ascii_uppercase[:6]}

def Find(node):
    if parentOf[node] != node:
        # path-compression
        parentOf[node] = Find(parentOf[node])
    return parentOf[node]

def Union (n1, n2):
    p1 = Find(n1)
    p2 = Find(n2)
    # union-by-rank 구현
    if rank[p1] < rank[p2]:
        parentOf[p1] = p2
    elif rank[p1] > rank[p2]:
        parentOf[p2] = p1
    else:
        rank[p1] += 1
        parentOf[p2] = p1

이제 이 함수를 이용해서 크루스칼 알고리즘을 구현하겠다.

크루스칼 알고리즘 구현

크루스칼 알고리즘은 저번에 설명했지만, 한번 더 짚고가겠다.

1. 모든 노드를 독립적인 집합으로 만든다.
2. 모든 간선을 비용 기준으로 정렬, 비용이 작은 간선을 선택한다.
3. 선택한 간선에 연결된 두 노드가 속한 집합이 다르다면(Find), 두 노드의 집합을 합치고(Union),
   간선을 트리에 추가한다.
4. 모든 간선에 대해 2번과 3번을 반복한다.

이렇게 해서 완성된 트리는 mst가 된다.

parentOf = {}
rank = {}

def Find(node):
    # 위 코드와 같음

def Union (n1, n2):
    # 위 코드와 같음

def Kruskal(graph):
    global parentOf, rank
    tree = []
    for node in graph['vertices']:
        parentOf = { v : v for v in graph['vertices'] }
        rank = { v : 0 for v in graph['vertices']}
    graph['edges'].sort()
    for edge in graph['edges']:
        if Find(edge[1]) != Find(edge[2]):
            Union(edge[1], edge[2])
            tree += [edge]
    return tree

mygraph = {
    'vertices': ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
    'edges': [
        (7, 'A', 'B'),
        (5, 'A', 'D'),
        (7, 'B', 'A'),
        (8, 'B', 'C'),
        (9, 'B', 'D'),
        (7, 'B', 'E'),
        (8, 'C', 'B'),
        (5, 'C', 'E'),
        (5, 'D', 'A'),
        (9, 'D', 'B'),
        (7, 'D', 'E'),
        (6, 'D', 'F'),
        (7, 'E', 'B'),
        (5, 'E', 'C'),
        (7, 'E', 'D'),
        (8, 'E', 'F'),
        (9, 'E', 'G'),
        (6, 'F', 'D'),
        (8, 'F', 'E'),
        (11, 'F', 'G'),
        (9, 'G', 'E'),
        (11, 'G', 'F')
    ]
}

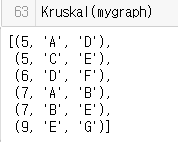
Kruskal(mygraph)

위에서 설명한대로 구현했다.

간선들을 정렬하고, 모든 간선들을 탐색하면서,
다른 집합일 경우 두 집합을 합치고, 트리에 추가

프림 알고리즘

시작 정점을 선택하고, 해당 정점을 포함하는 최소 신장트리를 구할 수 있다.

지금까지 연결된 노드들에 연결된 간선들 중 최소비용을 선택하여 확장해나가는 방식.
=> 이것 또한 탐욕 알고리즘 기반

프림 알고리즘 설명

1. 시작 노드를 선택
2. 선택된 노드를 “연결된 노드 집합”에 넣음
3. 선택한 노드와 연결된 간선들을 “간선 리스트”에 넣음
4. “간선 리스트”에서 최소 가중치를 가진 간선을 선택
5. 선택한 간선의 인접 노드가 “연결된 노드 집합”에 속하지 않는다면 해당 간선과 연결된 노드를 트리에 추가,
   해당 노드를 “연결된 노드 집합”에 추가, 해당 노드의 간선들을 “간선 리스트”에 추가
6. 선택한 간선을 “간선 리스트”에서 제거
7. “간선 리스트”에 간선이 없을 때까지 4번에서 6번 반복

다음 사진은 위의 과정을 그림으로 나타낸 예시.

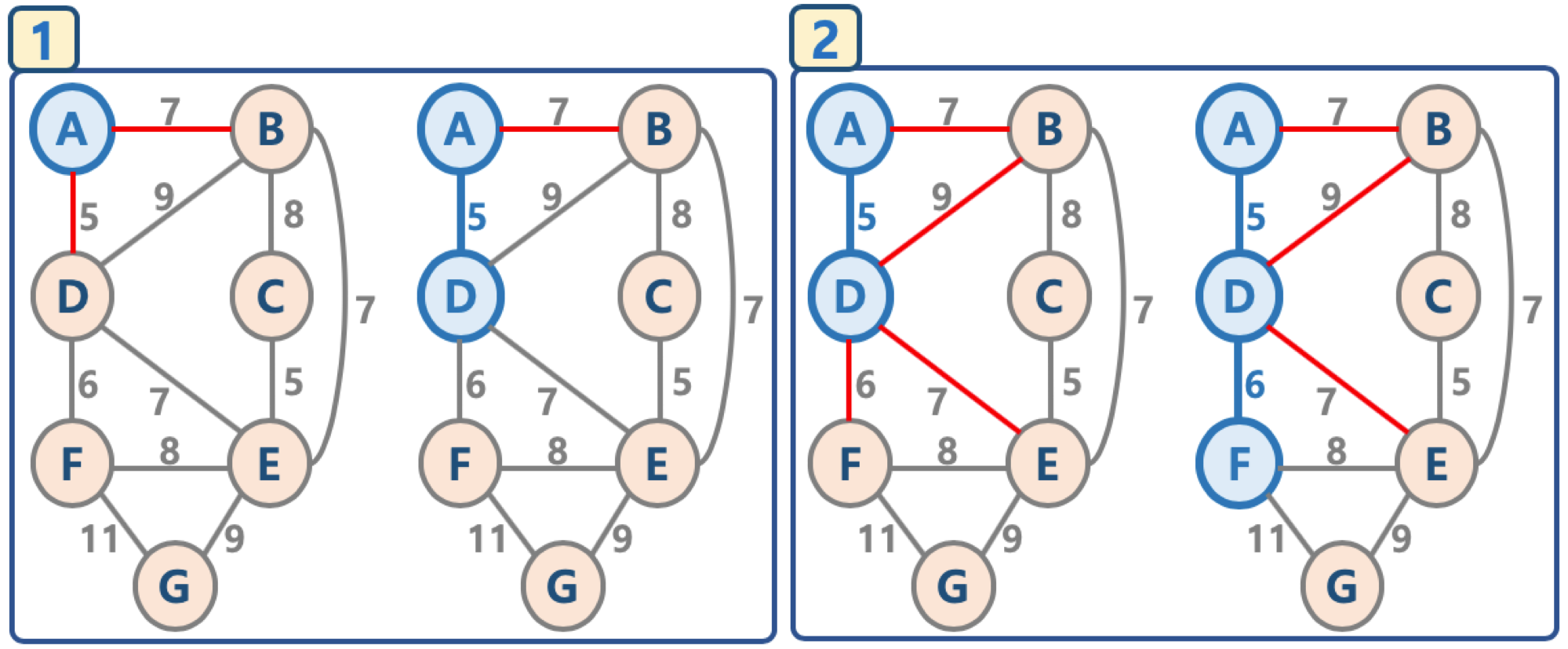
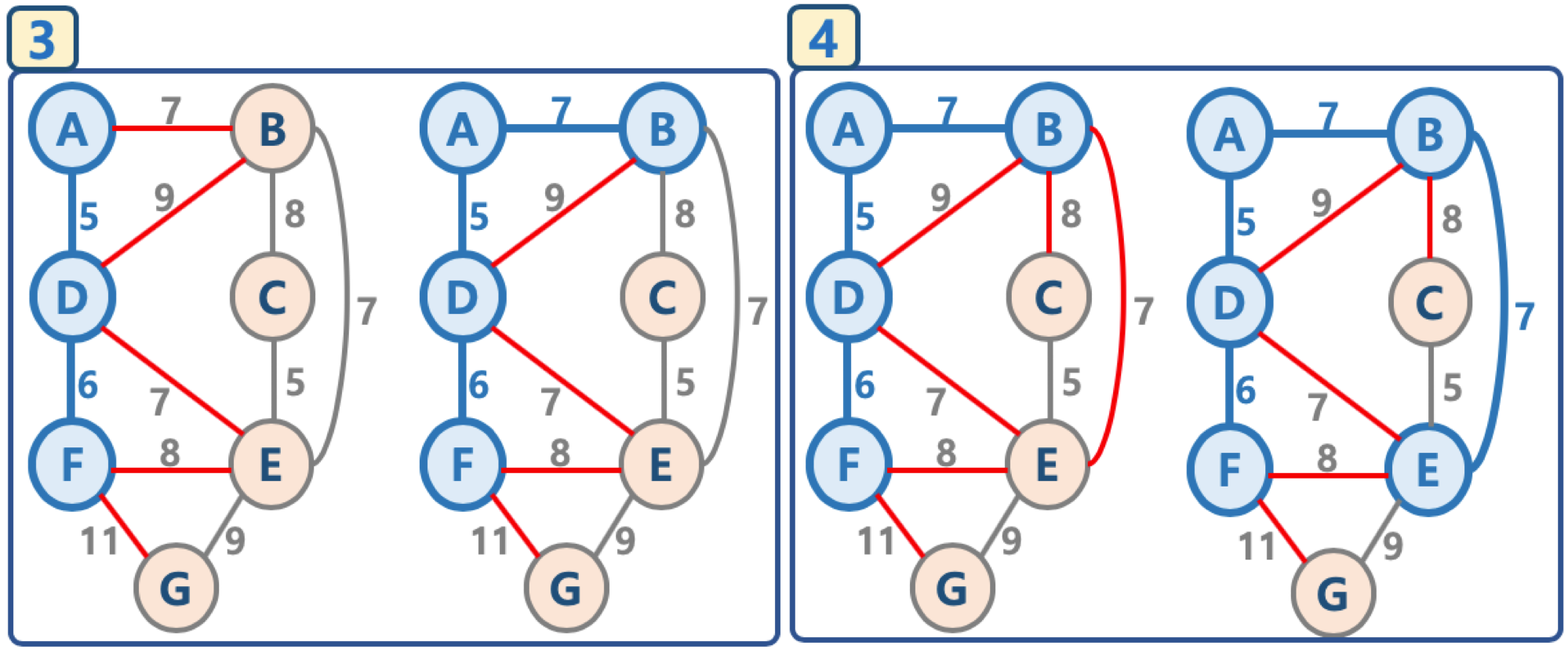
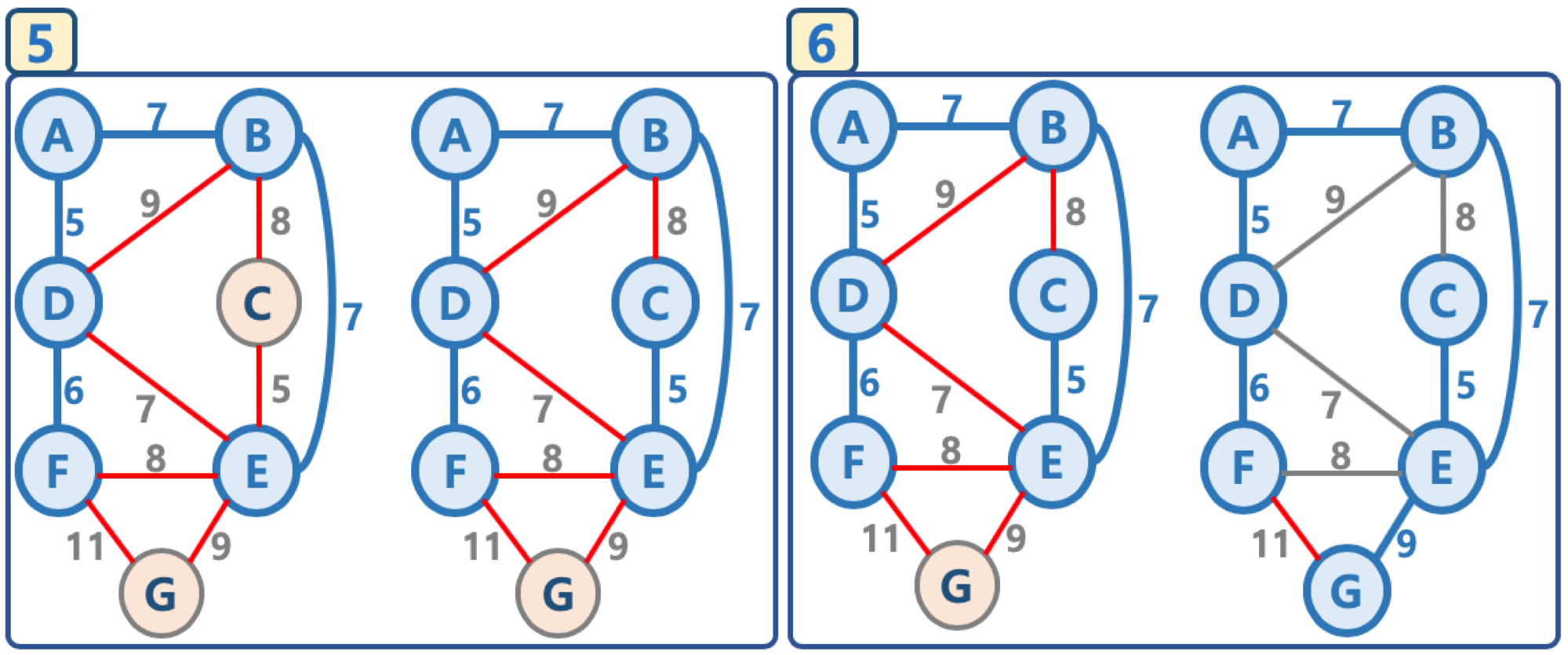
마지막

오늘 11시부터 작성하느라 12시전에 작성하기 빠듯했다.ㅠㅠ