자료구조/👉알고리즘 - 17

오늘 들은 강의 목록

1. 그래프 종류
2. 너비 우선탐색 - 1

무방향 그래프(Undirected Graph)

간선이 존재하면 양방향으로 이동 가능.

A와 B 연결시, A -> B, B -> A

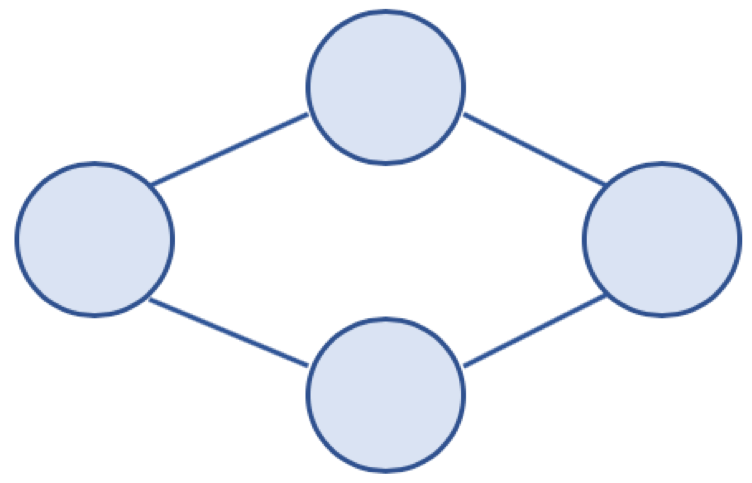
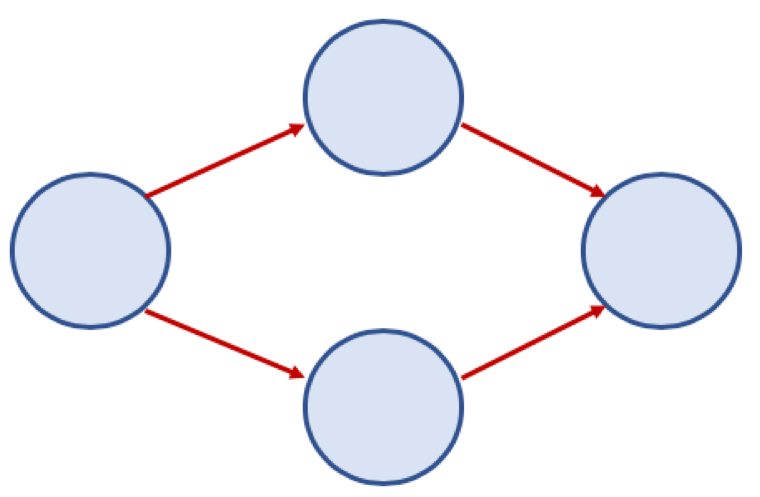
방향 그래프(Directed Graph)

방향이 있는 그래프

A -> B로 연결되면, B -> A로 이동은 불가능하다.

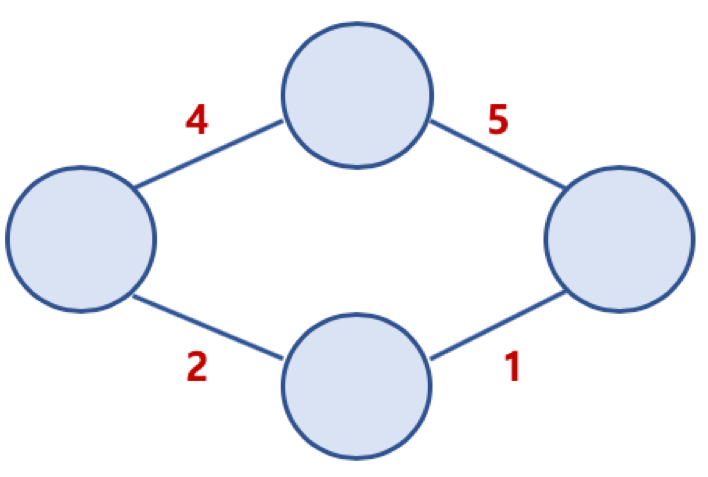
가중치 그래프(Weighted Graph) 또는 네트워크(Network)

간선에 비용(가중치)가 할당된 그래프

간선을 지나가기 위해서는 비용을 지불해야한다.
아래 사진에서 가장 왼쪽 노드에서 가장 오른쪽 노드로 가기 위해서는
9의 비용을 지불하거나 3의 비용을 지불해야한다.
따라서 최소의 비용으로 가는 방법은 아래쪽 노드를 거쳐가는 3의 비용을 지불하는 방법이다.
만약 간선을 지나갈때, 비용을 얻는 문제이고, 가장 큰 값을 찾으라 하면 9가 되겠다.
(비용을 지불하거나 거꾸로 얻을 수도 있다. 문제에 따라 다름)

연결 그래프(Connected Graph)

무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
(어떤 노드에서든 다른 모든 노드에 대해 접근 가능)

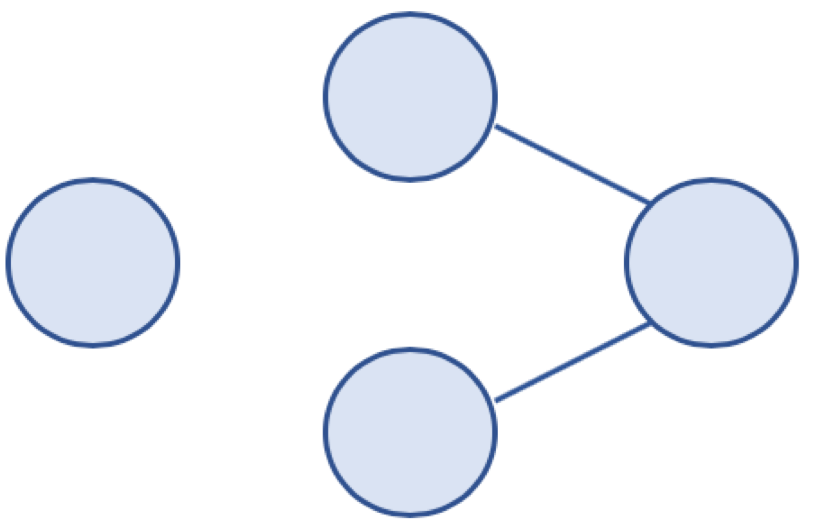
비연결 그래프(Disconnected Graph)

무방향 그래프에 있는 어떤 노드에 대해 경로가 존재하지 않는 경우
(도달할 수 없는 노드가 존재)

사이클(Cycle)

단순경로에서 시작노드와 종료 노드가 동일한 경우

비순환 그래프(Acyclic Graph)

사이클이 존재하지 않는 그래프

완전 그래프(Complete Graph)

모든 노드가 서로 연결되어있는 그래프

그래프 / 트리 차이

트리는 그래프 중에 속한 특별한 종류
트리는 비순환 방향 그래프라고 볼 수 있다.

그래프 종류 끝

여기까지는 그래프 종류고 그냥 적당히 알아두면 된다.

그래프 탐색(BFS, DFS)

그래프에서 탐색하는 기법은 크게 BFS, DFS로 나뉜다.

BFS(Breadth-First Search, 너비 우선 탐색) : 같은 레벨에 있는 노드들을 먼저 탐색함
DFS(Depth-First Search, 깊이 우선 탐색) : 한 노드의 자식을 타고 끝까지 가고, 다시 돌아와서 다른 형제의 자식을 타고 끝까지 가는 방식

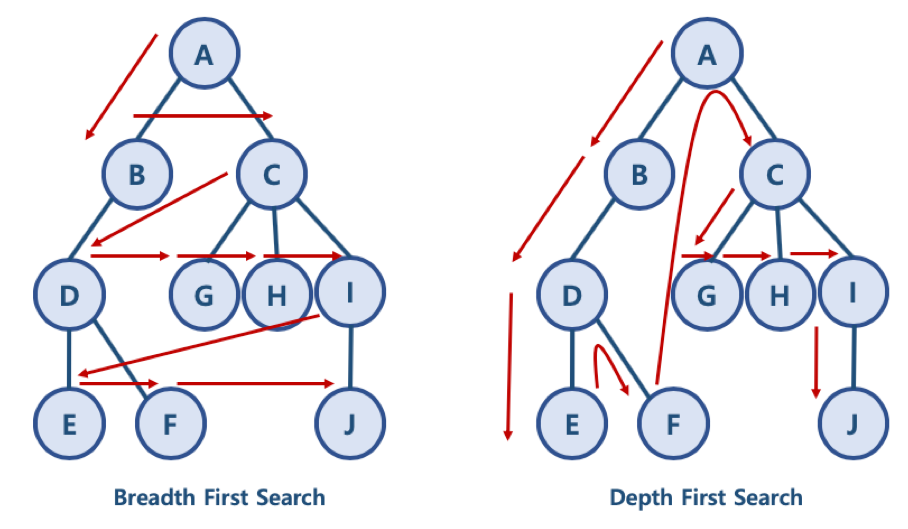
그래프 파이썬으로 표현

# 그래프 구현
graph = {}
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

그래프는 파이썬에서 딕셔너리 + 리스트를 사용한다.
어떤 노드를 딕셔너리의 Key, 인접 노드들을 value로 사용하는데,
인접 노드가 하나가 아닐 수 있으므로 value는 리스트를 사용해서 표현한다.
다른 방법들이 있지만, 이 구조 너무 편한 것..