boj19543-풀이
문제설명
던전은 $N$행 $M$열 크기의 격자로 이루어져 있고,
각 칸은 $R$, $U$로 이루어져있다.
$i$번째 행 $j$번째 열을 $(i, j)$이라 할때,
- $R$이 적혀있는 칸에서는 오른쪽으로 갈 수 있다. $(i,j)$ -> $(i, j + 1)$
- $U$가 적혀있는 칸에서는 위로 갈 수 있다. $(i,j)$ -> $(i+1,j)$
문자열로 이루어진 블록이 $K$개 주어진다.
각 블록의 길이는 $M$이고, 블록은 던전의 한 행을 나타낸다.
각 블록은 주어지는 순서대로 알파벳과 대응되며,
따라서 1번째 알파벳부터 $K$번째 알파벳까지 대응된다.
(K가 10인경우, 블록이 주어지는 순서대로 A,B,C,D,E,F,G,H,I,J가 대응됨)
$N$길이의 문자열이 주어지는데, 던전의 아래부터 구성되는 블록을 뜻하며,
문자열의 j번째 알파벳과 대응되는 블록이 던전의 아래에서 j번째 행이 된다.
입력
첫 번째 줄에 던전의 행 개수 $N$, 열 개수 $M$, 블록의 종류 $K$가 공백으로 구분되어 주어진다. ($1\le N,M \le 200000$, $1 \le K \le 26$ )
두 번째 줄부터 개의 줄에 R과 U로만 이루어진 길이 $M$의 문자열이 주어진다.
이 $K$개의 줄 중 $i$번째 줄은 $i$번째 알파벳 대문자에 대응되는 블록이다.(=>1번줄은 A에 대응되는 블록)
그 다음 줄에 알파벳 대문자의 처음 종류로만 이루어진 길이 $N$의 문자열이 주어진다.
이 문자열의 $j$번째 글자는 던전의 아래에서 $j$번째 행을 구성하는 블록을 의미한다.
출력
첫 번째 줄에 주어진 지도에서 $(N,M)$에 도달할 수 있는 시작 방의 개수를 출력한다.
$(N,M)$도 시작 방이 될 수 있음에 유의하라.
예시 및 설명
입력 1
3 4 3
RURU
RRUR
UURU
CBA
출력 1
7
풀이
혼자힘으로 못풀어서..TLETLETLE 핵심은 UCPC(?)풀이에서 보고 풀었다.

아래블록에서 보스의 방으로 갈 수 있는 방들을 구할 수 있다.
블록에서 보스의 방으로 갈 수 있는 방은 끊어지지 않고 이어지는 형태이다.
따라서 각 블록에서 보스의 방으로 갈 수 있는 방들의 좌표를 구간으로 나타낼 수 있다.
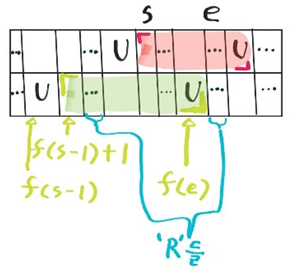
- 윗 블록에서 보스의 방으로 갈 수 있는 구간을 $[s, e]$(윗구간)라고 한다.
- $f(i)$는 x보다 왼쪽에 있는 U가 적혀있는 방들 중 가장 가까운 방의 좌표를 나타낸다고 한다.
- 아래 블록에서 보스의 방으로 갈 수 있는 구간을 나타내보면 $[f(s-1) + 1, f(e)]$가 된다. ($s \le f(e)$)
4구간으로 나눠보면,
[빨강, (주황 + 노랑), 초록, 파랑]
- $e < i$ (빨강)
$e < i$를 만족하는 어떤 $i$에 대해,
아래블록$i$의 위, 오른쪽에서 보스방에 도달할 수 없으면, 아래블록$i$에서도 보스방에 도달 할 수 없다.
=>구간 $[e+1,M]$에서는 도달불가$i$가 $i$의 최대값인 $M$일때, 윗 블록의 $M$번째 방에서 보스방에 도달할 수 없으므로 아래블록 $M$에서도 도달할 수 없다.
$i$가 $M-1$일때, 오른쪽 방인 $M-1$에서 보스방에 도달할 수 없고, 윗블록의 $M$번째 방에서 보스방에 도달할 수 없으므로 아래블록 $M-1$에서도 도달할 수 없다.
… $i$가 $e+1$일때, 윗 블록에서 $i$번째 방에서 보스방에 도달할 수 없고,
오른쪽 방에 해당하는 $i < k$인 어떤 방 $k$에서도 도달할 수 없다. 따라서 아래블록 $i$번째 방에서 보스방에 도달할 수 없다.
(수학적 귀납법에 의해 …이게 맞겠지?) - $s<x\le e$ (주황 + 노랑)
$s < x \le e$를 만족하고 ** 아래블록의 $x$번째 방들 중 방에 U가 적혀있는 방을 $x$라 할때의 최대값 $x$를 $i$라 할때,
$i$번째 방부터 왼쪽으로 보스방에 도달할 수 있다. (1)
$s\le j <i$인 어떤 $j$번째 방에서 보스방에 도달할 수 있다. (수학적 귀납법에 의해) 따라서 $s$번째 방부터 (1)을 뜻하는 $f(e)$번째 방까지 보스방에 도달할 수 있다.
=> 구간 $[s, f(e)]$ 도달가능, 구간 $[f(e), e]$ 도달불가$j$가 $i-1$일때, $i$번째 방에서 보스방에 도달가능 & 윗블록의 $i-1$번째 방에서 도달가능
$j$가 $i-2$일때, $i-1$번째 방에서 보스방에 도달가능 & 윗블록의 $i-1$번째 방에서 도달가능
…
$j$가 $s+1$일때, $s+2$번째 방에서 보스방에 도달가능 & 윗블록의 $s+2$번째 방에서 도달가능
$j$가 $s$일때, $s+1$번째 방에서 보스방에 도달가능 & 윗블록의 $s+2$번째 방에서 도달가능
(수학적 귀납법) - $i < s$
$i < s$를 만족하는 $i$에 대해,
$i$가 $s-1$일때, R이라면 $i$에서 도달가능
$i$가 $s-2$일때, R이라면 $i$에서 도달가능
…
$i$가 $n$일때, R이라면 $i$에서 도달가능
$i$가 $n-1$일때, U라면 도달불가
$n < i <s$을 만족하는 i번째방은 도달가능한 방이 되고,
이때의 $n$은 $f(s-1)$에 해당하므로 구간은 => 구간 $[f(s-1)+1, s]$은 도달가능
$n$번째 방과 그 왼쪽에 있는 방들은 도달불가능한 방이 된다.
=> 구간 $[1, f(s-1)]$은 도달불가
따라서 도달 가능한 구간은 $[f(s-1)+1, f(e)]$가 된다.
구현
후기?
핵심 풀이 사진한장 달랑보고 !아 이렇게도 풀 수 있구나 무쳣다 무쳤어 요런 느낌을 받았습니다
블로그 쓰면서 다시 풀어봐야겠다는 생각이 들었고
풀이코드를 보면 200ms걸렸는데 다른사람들은 100ms도 안걸린다..ㅠㅠ엉엉
다른사람들 코드 참고해서 뭐가다른지 봐야겠다는 생각이 들었습니다
풀이를 어떻게 써야 보기 쉬울까 하고 2일동안 수정했는데도 이정도라서 올릴까 말까 고민했는데
일단 올리고 나중에 수정을 하던지 해야겠다.

댓글남기기