boj1021-풀이

boj.kr/1021 회전하는 큐 (문제)

문제설명

---

n의 길이를 가진양방향 순환 큐가 존재하고,
이 큐에 할 수 있는 세가지 연산이 존재한다.
(큐는 초기에 $1$~$n$까지의 값을 가진다.)

1. 첫 원소를 뽑아낸다.
   이때, $a_1$~$a_n$ 큐는 $a_2$~$a_n$ 큐가 된다.
2. 왼쪽으로 한 칸 이동시킨다.
   이때, $a_1$~$a_n$ 큐는 $a_2$~$a_n, a_1$ 큐가 된다.
3. 오른쪽으로 한 칸 이동시킨다.
   이때, $a_1$~$a_n$ 큐는 $a_n, a_1$~$a_{n-1}$ 큐가 된다.

이 세가지 연산을 이용해서 뽑아내고자 하는 값(원소) k를 뽑아내는 구현문제다.

원소k를 뽑아내기 위해 최소한의 2, 3번 연산을 사용하도록 하고,
2, 3번 연산을 사용하는 횟수의 총 합을 구하는 문제!

풀이

---

제한시간도 넉넉하니 배열을 통해 구현을 통해 해결하도록 해보자!

(1번 방법, 정말 그대로 회전시키고 뽑아내는 방법)

1. 가까운 방향으로의 회전
   2, 3번 연산을 최소한으로 사용하기 위해서는 $k$를 찾고,
   가장 가까운 끝쪽을 찾아서 그 방향으로 회전시켜야한다.
   $k$의 위치를 $idx$라고 하면,
   왼쪽 끝과의 거리는 $idx$, 오른쪽 끝과의 거리는 $n - idx$이다.
   하지만, 오른쪽 회전 연산의 횟수는 오른쪽 끝과의 거리 + 1로 정리하자면,

좌측 회전 연산 횟수 : $idx$
우측 회전 연산 횟수 : $n - idx + 1$

1. 뽑아내기
   최대 길이를 1 줄이고, 배열을 한칸씩 왼쪽으로 밀어준다.

(2번 방법, 한번에 모아서 회전)
위 방법에서 한방향으로 $idx$번 또는 $n - idx + 1$번 반복되는 회전을 한번에 하려면,
원소$k$ 기준으로 앞과 뒤로 나눌 수 있다.
구간을 나타내보면, $[0, idx)$, $[idx + 1, n)$
회전을 마치게 되면 이 두 구간은 서로 엇갈리게 된다.

예시 1) 1 2 3(x) 4 5 -> 4 5 1 2
예시 2) 1 2(x) 3 4 5 -> 3 4 5 1
예시 2) 1 2 3 4(x) 5 -> 5 1 2 3
예시에서 처럼 좌측회전이든 우측회전이든 상관없다.

어떻게 움직이는지 보자

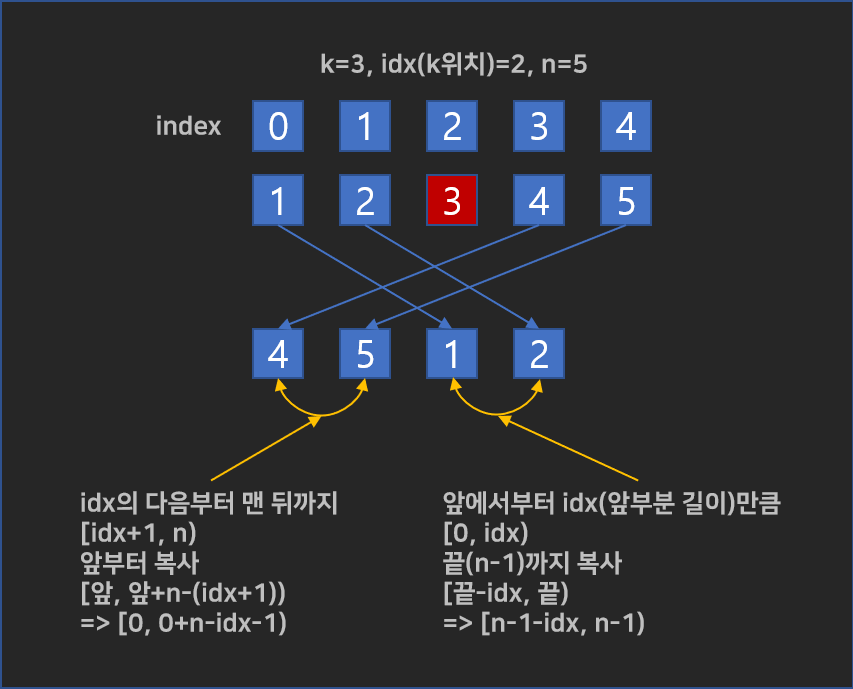
$[0, idx)$ -> $[n - 1 - idx, n - 1)$
$[idx + 1, n)$ -> $[0, n - idx - 1)$
이대로 복사하는 부분을 변경해주면 된다.

구현

---

#include <bits/stdc++.h>
using namespace std;

int arr[50], cpa[50];
int n, k, result = 0;

int main() {
	cin >> n >> k;
	for (int i = 0; i < n; ++i)
		arr[i] = i + 1;
	for (int i = 0; i < k; ++i) {
		int t;
		cin >> t;
		int idx = 0;
		for (int j = 0; j < n; ++j) {
			if (arr[j] == t) {
				idx = j;
				break;
			}
		}
		if (idx < n - idx) {
			result += idx;
		}
		else {
			result += n - idx;
		}
		for (int j = 0; j < n; ++j) {
			cpa[j] = arr[j];
		}
		for (int j = 0; j < idx; ++j) {
			arr[n - 1 - idx + j] = cpa[j];
		}
		for (int j = idx + 1; j < n; ++j) {
			arr[j - idx - 1] = cpa[j];
		}
		--n;
	}
	cout << result;
	return 0;
}

TMI

---

전역전 휴가~ :)