ABC222-풀이
A - Four Digits
문제설명(A)
0~9999 사이의 정수가 주어질 때,
항상 4자리가 되도록 앞에 0을 추가하여 출력하는 문제
풀이(A)
- 4자릿수 : 1000으로 나누어 몫이 있음 ($n = k*10^3 + p$)
- 3자릿수 : 100으로 나누어 몫이 있음
- 2자릿수 : 10으로 나누어 몫이 있음
- 1자릿수 : 0이 아님
- 0
위 조건대로 조건문을 구성해서 출력하면 된다.
(자세한 설명은 생략한다. 코드 보는게 더 빠름)
구현(A)
int main() {
int n;
cin >> n;
if (n / 1000) cout << n;
else if (n / 100) cout << "0" << n;
else if (n / 10) cout << "00" << n;
else if (n) cout << "000" << n;
else cout << "0000";
return 0;
}
B - Failing Grade
문제 설명(B)
n개의 점수들이 주어지고,
p미만인 점수의 수를 출력하는 문제
풀이(B)
두가지 방법이 존재
- 저장 후, 비교 (메모리 넉넉하게 주어져서 상관없다.)
- 입력받자마자 비교
구현(B)
int main() {
int n, p;
cin >> n >> p;
int a;
int c = 0;
for (int i = 0; i < n; ++i) {
cin >> a;
if (a < p) ++c;
}
cout << c;
return 0;
}
C - Swiss-System Tournament
문제 설명(C)
구현문제
$2N$명이 $M$라운드동안 1:1로 가위바위보 게임을 한다.
각 라운드가 끝나면 아래 규칙에 따라 랭크(순위)가 정해진다.
$i$번째 라운드가 끝날 때,
승수가 높으면 높은 순위
작은 id값을 가진 사람이 높은 순위
(id는 맨 처음 시작할때, 처음 사람부터 $1$~$N$까지 부여된다.)
(순위 결정방식을 해석을 못해서 못풀었다..)
순위 -> 랭크로 그룹짓는줄 알았는데 그냥 순위였던 것
각 $i$번째 라운드에 대해서 매칭은 다음과 같이 진행된다.
$(i-1)$번째 라운드 기준으로,
$k=1,2,3,…,N$인 k에 대해서 $(2k-1)$번째 순위의 사람과 $2k$번째 순위의 사람이 매칭된다.
풀이(C)
- 라운드 시작
- $k=1,2,3,…,N$에 대해 $(2k-1)$과 $2k$번째 사람 매칭
- 가위바위보 진행, 이긴사람에게 승수 추가
- 승수와 id를 기준으로 순위별로 정렬 위 과정을 반복하도록 구현하면 된다.
구현(C)
#include <bits/stdc++.h>
using namespace std;
#define pii pair<int, int>
#define rank first
#define id second
int n, m;
string gcp[100]; // 가위바위보 문자열 (초기 순서 유지, id값으로 접근)
pii players[100]; // 플레이어 정보 {id, rank} (계속 변경됨, 정렬됨)
int checkWin(char f, char l) {
return (f == 'G' && l == 'C') || (f == 'C' && l == 'P') || (f == 'P' && l == 'G');
}
int main() {
cin >> n >> m;
for (int i = 0; i < n * 2; ++i) {
cin >> gcp[i];
players[i].id = i;
players[i].rank = 0;
}
for (int i = 0; i < m; ++i) {
// 가위바위보 진행
for (int k = 0; k < n; ++k) {
int f = players[k * 2].id, l = players[k * 2 + 1].id;
char fc = gcp[f][i], lc = gcp[l][i];
if (fc != lc) {
if (checkWin(fc, lc))
players[k * 2].rank += 1;
else
players[k * 2 + 1].rank += 1;
}
}
// 랭크 정렬
sort(players, players + n * 2, [](pii& a, pii& b) {
if (a.rank != b.rank)
return a.rank > b.rank;
else
return a.id < b.id;
});
}
for (int i = 0; i < n * 2; ++i)
cout << players[i].id + 1 << endl;
return 0;
}
D - Between Two Arrays
문제 설명(D)
$n$개의 숫자로 이루어진 수열 $S = (s_1, s_2,…, s_n)$은 모든 $i(i \le i \le n - 1)$에 대해 $s_i \le s_{i+1}$를 만족해야만 단조 증가 수열(비감소 수열)이라고 한다.
각각 $N$개의 정수로 이루어진 단조 증가 수열이 주어진다.
$A = (a_1, a_2,…,a_N)$
$B = (b_1, b_2,…,b_N)$
다음 조건을 만족하는, $N$개의 수열로 이루어진 단조 증가 수열들의 수를 찾아라.
- 모든 $i(1 \le i \le N)$에 대해서 $a_i \le c_i \le b_i$
결과값은 $998244353$로 나눈 나머지를 출력.
풀이(D)
요약하자면
두 수열 $A, B$가 주어질때,
각 수열의 $i$번째 요소 $a_i$, $b_i$가 있다.
$c_i$는 $a_i \le c_i \le b_i$를 만족해야 하고, 이러한 조건을 만족하는 $c_i$를 찾아서 수열을 구성하면 되는 문제
전형적인 DP문제
- DP문제라고 생각한 이유
- 첫 생각은, 격자에서 a에서 b까지 가는 경로의 수 문제랑 비슷하다고 생각함
- 각 $i$번째 단계에서 $c_i$를 결정할 때, $a_i$부터 $b_i$까지의 수$n$을 선택해야하고,
이전 단계의 선택 결과를 통해 현재 $i$번째 단계의 $n$을 골랐을 때 수열의 수를 결정할 수 있다.
-> 최적부분구조가 성립된다고 생각
$A = 1, 2, 3, 4$
$B = 1, 3, 5, 7$
이렇게 두 수열이 주어질 때,
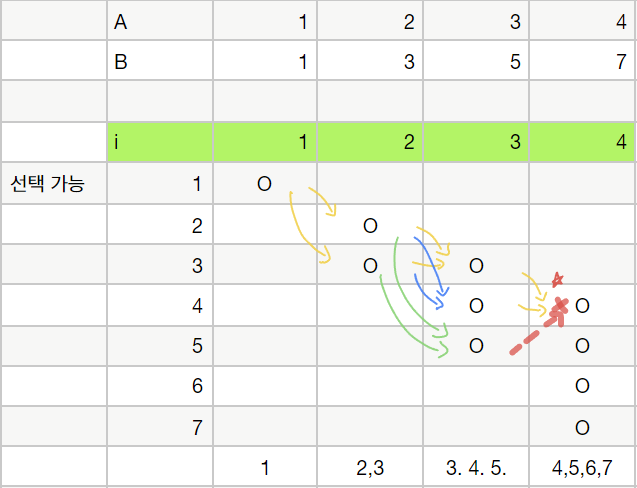
각 $i$번째 단계에서 선택가능한 수들을 찾아보면 아래 사진과 같다.
(선택 가능한 수 = $c_i$가 될 수 있는 수 = $a_i \le c_i \le b_i$를 만족하는 수)
$i$번째 단계에서 선택가능한 수$j$를 마지막으로 선택했을때,
만들어지는 수열의 가짓수를 $(i, j)$라고 하겠다.
- 1번째 단계에서
- 1을 선택했을 때, 만들어지는 수열의 가짓수는 1개 (1)
- 2번째 단계에서
- 2를 선택했을 때, 1개 [1, 2]
- 3을 선택했을 때, 1개 [1, 3]
- 3번째 단계에서
- 3을 선택했을 때, 2개 [1, 2, 3] [1, 3, 3]
- 4를 선택했을 때, 2개 [1, 2, 4] [1, 3, 4]
- 5를 선택했을 때, 2개 [1, 2, 5] [1, 3, 5]
- 4번째 단계에서
- 4를 선택했을 때, 4개 [1, 2, 3, 4] [1, 3, 3, 4], [1, 2, 4, 4] [1, 3, 4, 4]
지금까지는 이전 단계$i-1$에서의 합이 현재 단계에서 어떤 수$j$를 선택했을때 만들어지는 수열의 가짓수가 되었다.$(i,j) = \displaystyle \sum_{k=a_{i-1}}^{b_{i-1}}{(i-1,k)}$
하지만 여기서는 다르다.
단조 증가 수열을 이뤄야하기 때문에, 모든 $i$에 대해서 $c_i \le c_{i + 1}$를 만족해야하므로,
(쉽게말해 이전단계에 선택한 수보다 현재단계에 선택한 수가 크거나 같아야한다.)
$j$가 $b_{i-1}$보다 작은 경우, $(i,j)$는 이전단계의 모든 결과의 합이 아닌,
현재단계에서 선택하고자 하는 수($j$, 여기에서4)까지의 합이 되어야한다.
-> $b_{i - 1}$ 또는 $j$ 중 더 작은 수까지의 이전 단계 결과의 합이 되어야함.$(i,j) = \displaystyle \sum_{k=a_{i-1}}^{min(b_{i-1}, j)}{(i-1,k)}$
- 5를 선택했을 때, 6개
- 6을 선택했을 때, 6개
- 7을 선택했을 때, 6개
- 4를 선택했을 때, 4개 [1, 2, 3, 4] [1, 3, 3, 4], [1, 2, 4, 4] [1, 3, 4, 4]
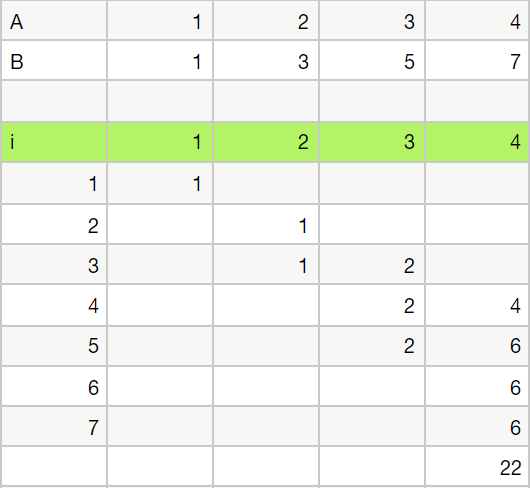
- 4번째 단계에서 만들 수 있는 수열의 갯수의 합 = 22
우선 가장 간단한 점화식이 하나 나왔다.
$(i,j) = \displaystyle \sum_{k=a_{i-1}}^{min(b_{i-1}, j)}{(i-1,k)}$
그러나 각 단계 $i$에서 $a_i \le j \le b_i$를 만족하는 모든 $j$에 대해서,
합계를 구하는 방법이 최선일까?
(모든 $(i,j)$에 반복문 안돌리려면 모든$i$, $j$에 대해 $(i,j) = (i-1, j) + (i, j-1)$.
$3000^2$밖에 안나옴..)
$j < b_{i -1}$의 경우를 생각해보자.
$(i,j) = (i-1, a_{i-1}) + (i-1, a_{i-1} + 1) + … + (i-1, j)$
$(i,j + 1) = (i-1, a_{i-1}) + (i-1, a_{i-1} + 1) + … + (i-1, j + 1)$
$(i, j) - (i, j + 1) = (i-1, j + 1)$
이렇게 정리할 수 있다.
따라서, $i$단계의 가장 첫 원소는 반복문을 돌리되,
이후에는 $(i,j) = (i-1, j) + (i, j-1)$이 점화식을 적용한다.
(시간 넉넉하게 주어질때는 쉬운걸로 호다닥 풀자..)
정리
$j(0 \le N),\space i(a_i \le i \le b_i)$ 에 대해
$DP[j][i] = \begin{cases} = 1 & if \space (j = 0)
{\displaystyle\sum_{k=a_{j-1}}^{i}{DP[j-1][k]}} &(if \space a_i = i)
DP[j-1][i] + DP[j][i-1] &(if \space a_i \lt i, 항상 만족) \end{cases}$
($a_i = i$에서 걸러지면 $a_i \lt i$는 항상 만족됨)
구현(D)
int n;
int dp[3001][3001];
int a[3000], b[3000];
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 0; i < n; ++i) cin >> a[i];
for (int i = 0; i < n; ++i) cin >> b[i];
for (int i = a[0]; i <= b[0]; ++i) dp[0][i] = 1;
for (int j = 1; j < n; ++j) {
int i = a[j];
for (int k = a[j - 1]; k <= i; ++k) {
dp[j][i] = (dp[j][i] + dp[j - 1][k]) % 998244353;
}
for (++i; i <= b[j]; ++i) {
dp[j][i] = (dp[j - 1][i] + dp[j][i - 1]) % 998244353;
}
}
int res = 0;
for (int i = a[n - 1]; i <= b[n - 1]; ++i) {
res = (res + dp[n - 1][i]) % 998244353;
}
cout << res;
return 0;
}
댓글남기기