유니온 파인드(Union Find)

유니온 파인드(Union Find)

목차

1. Union
2. Find
3. 최종 소스코드

간단한 소개

---

Union : 두 원소가 포함된 각각의 두 집합을 하나의 집합으로 합침 (집합 : 트리, 그룹 등)

Find : 원소가 속한 집합의 대표 원소를 반환 (원소 : 노드, 대표 원소 : 최상위 노드)

Disjoint-set 자료구조를 만들때 사용되는 알고리즘

각 노드는 부모노드를 가리킨다.

처음에는 자기자신을 가리키도록 한다.

자기자신을 루트로 하는 각각의 독립된 트리로 초기화하는 것

// 0.PNG의 parent구조
parent[6] = {0, 1, 2, 3, 4, 5}; // 이러한 형태로 자기자신을 가리키도록 한다.

1. Union

---

2-1. Union 기본
2-2. Union 구현 (기본)
2-3. 최적화 : union-by-rank
2-4. Union 최적화 구현 (union-by-rank)

2-1. Union 기본

---

두 노드가 주어질 때, 각 노드가 포함된 트리의 최상위 노드를 찾아 합친다.

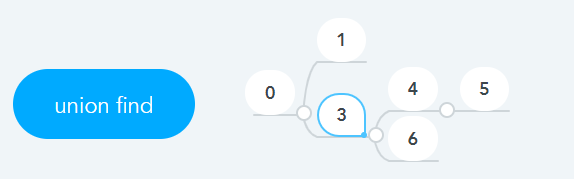
// 1.PNG의 parent구조, Union(0, 1), Union(0, 2), Union(3, 4), Union(3, 5)
parent[6] = {0, 0, 0, 3, 3, 3};

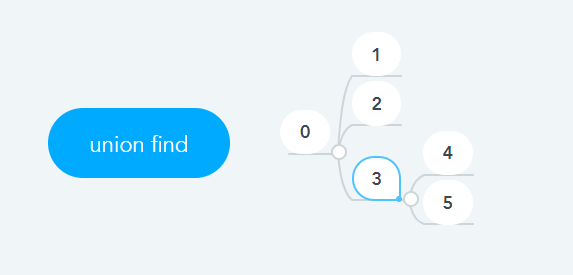
위 그림(1.PNG)에서 두 노드 (2, 5)에 대해 Union하면,

2의 최상위 노드인 0과, 5의 최상위 노드인 3을 연결하게 되어 아래와 같이 바뀐다.

// 2.PNG의 parent구조, Union(2, 5)
parent[6] = {0, 0, 0, 0, 3, 3};

2-2. Union 구현 (기본)

---

void Union(int f, int s){
    f = find(f);
    s = find(s);
    parent[s] = f;
}

2-3. 최적화 : union-by-rank

---

각 노드가 깊이를 뜻하는 rank를 가지며,
Union할때 rank가 더 큰 노드가 루트가 되도록 한다.

rank는 1로 초기화한다. (초기에는 자기자신을 루트로하는 깊이가 1인 트리구조를 띄기 때문) rank가 증가하는 경우는 같은 높이의 트리를 합칠때다. (적어도 하나의 트리의 rank가 증가함)

rank는 기본적인 union find구현에 포함되지 않으며, union-by-rank 최적화에 포함된다.

아래 그림에서 find(9)를 하면, 노드를 3번 거쳐서 결과가 나온다.

rank[0] = 2
rank[3] = 3

아래 그림에서 find(9)를 하면, 노드를 4번 거쳐서 결과가 나온다.

rank[0] = 4
rank[3] = 3

아래 그림에서 find(9)를 하면, 노드를 3번 거쳐서 결과가 나온다.

rank[0] = 2
rank[3] = 3

위 예시들에서 보이듯이 최적화 되지 않은 경우, find(9)에서 거쳐야할 노드가 더 많아졌음을 알 수 있다.

2-4. Union 최적화 구현 (union-by-rank)

void Union(int f, int s){
    f = find(f);
    s = find(s);
    if(rank[f] < rank[s]) // f에 더 큰 rank를 가진 노드가 오도록 함
        swap(f, s);
    if(rank[f] == rank[s]) // 같은 랭크의 경우 루트가 될 집합에 랭크 추가
        ++rank[f];
    parent[s] = f;
}

2. Find

---

2-1. Find 기본
2-2. Find 구현 (기본)
2-3. 최적화 : 경로압축(Path Compression)
2-4. Find 구현 (경로압축, Path Compression)

2-1. Find 기본

---

주어진 노드가 속한 트리의 최상위 노드를 반환한다.

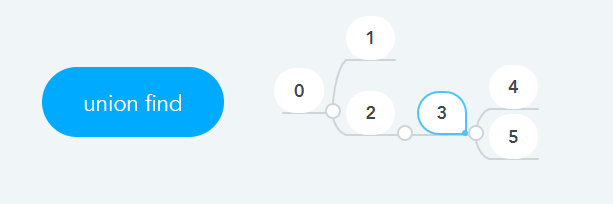
// 3.PNG의 parent구조
parent[7] = {0, 0, 0, 2, 3, 3};

위와 같은 구조에서 Find(5)를 하게 되면,
5의 부모노드 3 -> 3의 부모노드 2 -> 2의 부모노드 0 -> 0의 부모노드 0(자기자신)

2-2. Find 구현 (기본)

---

int Find(int i){
    if(parent[i] == i) // 자기자신이 부모인 경우, 최상위 노드임
        return i;
    return Find(parent[i]);
}

2-3. 최적화 : 경로압축(Path Compression)

---

주어진 노드로부터 최상위 노드까지 경로에 있는 모든 노드들의 부모 노드를 최상위 노드로 갱신한다. 즉, Find(5)를 하면 경로에 있던 모든 노드들의(2, 3, 5) 부모노드는 최상위 노드로 갱신된다.

// 3.PNG의 parent구조
parent[7] = {0, 0, 0, 2, 3, 3};

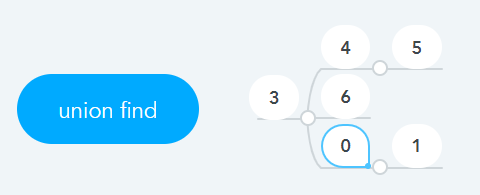
아래는 경로압축이 들어간 find(5)를 하고 난 결과

// 4.PNG의 parent구조
parent[7] = {0, 0, 0, 0, 3, 0};

2-4. Find 구현 (경로압축, Path Compression)

---

int Find(int i){
    if(parent[i] == i) // 자기자신이 부모인 경우, 최상위 노드임
        return i;
    return parent[i] = Find(parent[i]); // 최상위노드로 갱신
}

3. 최종 소스코드

---

// parent는 자기자신으로 초기화된 상태. parent[i] = i
// rank는 1로 초기화된 상태

int Find(int i){
    if(parent[i] == i) // 자기자신이 부모인 경우, 최상위 노드임
        return i;
    return parent[i] = Find(parent[i]); // 최상위노드로 갱신
}

void Union(int f, int s){
    f = find(f);
    s = find(s);
    if(rank[f] > rank[s]) // f에 더 작은 rank가 오도록 함
        swap(f, s);
    if(rank[f] == rank[s]) // 같은 랭크의 경우 루트가 될 집합에 랭크 추가
        ++rank[f];
    parent[s] = f;
}